今日は、少し難しいお話をします。
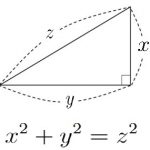
中学校３年生で「三平方の定理」を習います。直三角形の「短い辺の長さ」をそれぞれ２乗してたすと、「斜辺の長さ」の２乗になる。という定理です。例えば、右の図で、「ｘ=３㎝、ｙ=４㎝、ｚ=５㎝」の三角形は、
９(3×3)+16(4×4)＝25(5×5)となり、直三角形である。という定理です。
こんなｘ，ｙ，ｚの組み合わせは、他に何があるのでしょう。私もいくつかは知っていますが、ネットで調べると複数個組み合わせが出てきました。
（他例 a=７㎝、b=24㎝、c=25㎝ ）
その授業の最後に、数学の先生から「２乗を３乗にして、成り立つ整数の組み合わせはあるのか？」「見つけたら有名人になれる。」と言われ、しばらく、いろいろな組み合わせを試してみたことがあります。後からわかったことですが、これが「フェルマーの最終定理」というやつで、結論から言うと、３乗以上の場合、ｘｙｚの自然数（1,2,3,・・・)の組み合わせは存在しない。ということが証明されています。
この定理、簡単な数式なのに、発表から350年以上、誰も証明できなかった難問で、1995年の2月13日にようやく証明されました。私が中学生の時はまだ、証明されていなかったので、数学の先生の言ったことは、まんざら間違ってはいなかったのですが、「ない」と証明されな数字の組み合わせを、いろいろ考えていた時間はいったい何だったんだろう。と少しもやもやします。
今日の南陵日記は、完全に個人的な内容になってしまい、数学が苦手な方にとっては、ただただ小難しい話だったと思います。大変申し訳ありませんでした。
南陵公民館
